世の中にはいろいろな形の立体があり、それらがどれくらいの大きさなのかを把握するのに「体積」、「表面積」を用います。立体というだけで、苦手になるお子さまが多くなるのですが、円柱の体積や表面積を求めるには、円の面積や円周の長さの求め方が必要で、さらに苦手なお子さまが多くなります。ここでしっかりと確認しておきましょう。
円柱の体積・表面積をしっかりマスター!中学生の個別指導はこちら⇒

LINE友だち追加で、受験&勉強の最新情報をGET!!
受験や勉強の最新情報をギュっと凝縮した記事を配信中♪学習のお悩みを解決するヒントとなる記事や、東京個別・関西個別からのお知らせもお届け。ぜひご登録ください。
目次
円柱の体積の求め方は?
「円柱」ってどんな立体?
「●●柱」と呼ばれる立体は、上と下の底面が同じ形をしています。下の図の立体は、底面の形が円なので「円柱」といいます。
中学1年では、下の図の立体のような「●●錐」と呼ばれる立体を学びます。底面の形が円なので、「円錐」といいます。
円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。
「円柱」の体積を求めてみよう!
●例題
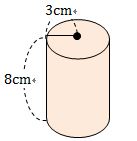
底面の円の半径が 、高さが 8 である円柱の体積を求めなさい。ただし、円周率はπとする。
まず、「●●柱」の体積の求め方を確認しましょう。
| (●●柱の体積) = (底面積) × (高さ) |
でしたね。
円柱の底面は「円」ですから、
| (円柱の体積) = (底面の円の面積) × (高さ) |
ですね。
では、「円の面積の求め方」も確認しましょう。これは大事な公式ですからしっかりと覚えておきましょう。
円の面積の求め方は、
| (円の面積) = (半径) × (半径) × (円周率π) |
ですね。
ここまでわかれば、準備完了です。
・底面の円の面積は 3×3×π=9π㎡
・高さは 8cm
よって、求める円柱の体積は、9π×8=72π㎥
中学生になると、円周率πを使えて「」の計算をしなくて良い場合が多くなって楽になりますが、文字式のルールに従った書き方をしましょう。また、答えを書くときは単位を忘れないようにしましょう。
個別指導塾の基本問題に挑戦!
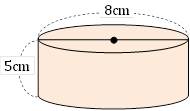
次の円柱の体積を求めなさい。
(1)
底面の円の半径が
5cm で、高さが10cm
(2)
■問題
□答え
(1)
底面の円の面積は、
5×5×π=25π㎡
高さは
10cmなので、25π×10=250π㎥
(2)
図より、底面の円の直径が
8cmだから、半径は4cm底面の円の面積は、4×4×π=16π㎡
高さは
5cmなので、16π×5=80π㎥
※(2)は直径が与えられていることに注意!半径は直径の半分!
円柱の体積の公式 V=πr2hって?
円柱の体積の求め方を確認したところで、円柱の体積の公式についてふれておきましょう。
| ある円柱において、底面の円の半径をr 、高さをh、その円柱の体積を Vとすると、V=πr2h |
この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。
(底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr2
(円柱の体積)=(底面の円の面積)×(高さ)=πr2×h= πr2h
円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。上の基本問題をこの公式を使って求める
(1) r=5、h=10 だから、V=π ×52×10=250π cm3
(2) r=4、 h=5 だから、V=π×42×5=80π cm3
「これを覚えれば楽ちん」って思うお子さんもいるかもしれません。しかし、これだけでは、三角柱や四角柱などの他の柱体の体積を求めるときに困ってしまいます。きちんと順番通りに求める方法を必ず覚えましょう。余力がある人は公式を覚えてしまうといいでしょう。
円柱の表面積の求め方は?
表面積を求めるには、展開図を考えよう!
●例題
底面の円の半径が 3cm 、高さが 8cm である円柱の表面積を求めなさい。ただし、円周率はπとする。

次に、円柱の表面積を求めていきましょう。立体の表面積を求めるには、底面積と側面積の体積を足せばよいのです。しかし、円柱の側面は、この図から考えるのはちょっと難しいですね。
そこで、「展開図」を書いてみましょう。すると、このようになります。

つまり、側面積は長方形であり、たての長さが とわかりますね。問題は、よこの長さです。図の赤い太線に注目しましょう、この2つの赤い太線はもともとくっついていたところです。つまり、この長方形のよこの長さを求めるには、底面の円周の長さを求めればいいのです。
では、円の円周の長さの求め方がわからなくてはなりませんね。
円周の長さは、
| (円周の長さ) = (直径) × (円周率) |
です。
「半径」ではなくて「直径」であることに注意しましょう。
問題で与えられているのは「半径」で だから、「直径」は2倍のです。これで展開図の長方形のよこの長さがわかり、求めたい円柱の側面積がわかりますね。
- 底面の円周(長方形のよこの長さ)は 2×3×π=6π cm
- 円柱の側面積は 8×6π=48π cm2
- 底面積は 3×3×π=9π cm2
ここで、底面は上下2つあることに注意しましょう。
よって、求める表面積は、2×9π+ 48π=66π cm2
個別指導塾の基本問題に挑戦!
■問題
底面の円の半径が で、高さが の円柱の表面積を求めなさい。
□答え
展開図は右図のようになる。
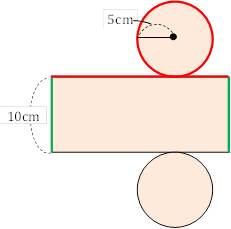
- 底面の円周は 2×5×π=10π cm
- 円柱の側面積は 10× 10π=100π cm2
- 底面積は 5×5×π=25π cm2
よって、求める表面積は、2×25π+100π=150π cm2
個別指導塾の応用問題に挑戦!
それでは最後に、実力をつけていくための問題に挑戦しましょう。
■応用問題
下の図のような長方形ABCDがある。長方形ABCDを、直線ADを軸として1回転させてできる立体の、体積と表面積を求めなさい。
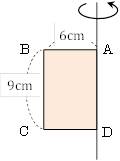
□答え
体積:324π cm3
応用問題が解けなかったお子さんは、「どこがわからないのか」を特定し、基礎からステップを追って確実に復習することが大切です。
今回は円柱の体積・表面積について解説をしました。この内容については、
・円の面積や円周の長さの求め方がわからない
・円柱の展開図を書くことができない。
など、つまずくポイントはお子さんによってさまざまです。場合によっては算数の内容にさかのぼって復習をする必要があるかもしれません。
数学は「積み上げ学習」と言われており、以前の学年で習った内容をもとに、発展した学習を積み上げていきます。特に、今回学んだ、円柱の体積・表面積の求め方は円錐の体積・表面積の求め方をはじめ今後の学習内容を学んでいく上での前提にもなります。できるだけ「わからない」を残さないように、きちんと身に付けておきましょう。
中学生の個別指導
目標達成を自分のペースで。1人ひとりに最適な学習プランを組み立て、着実なステップアップを応援します。高校受験、私立補習・内部進学、定期テスト、英検対策までお任せください。