算数や数学では、物の数や面積など、いろいろな数を扱っていきます。数で表すと数量の関係がはっきりするので、物事を正確に考えることができるようになるのです。その数量の関係を表すときに使う記号には「等号」や「不等号」があります。
「等号」とは「=」のことで、数量が等しいときに使います。「不等号」には「>」「<」「≧」「≦」があります。この4つの記号を正しく把握して扱えるようになることで、数学の理解が圧倒的に深まります。そこで不等号が表す意味や使い方について確認をしておきましょう。

LINE友だち追加で、受験&勉強の最新情報をGET!!
受験や勉強の最新情報をギュっと凝縮した記事を配信中♪学習のお悩みを解決するヒントとなる記事や、東京個別・関西個別からのお知らせもお届け。ぜひご登録ください。
目次
「 > 」「 < 」「 ≧ 」「 ≦ 」の意味と違いは?
どちらが大きいかは口の開き方に注目しよう!
「 > 」「 < 」は比べるものの大きさが等しくないときに使われます。 つまり、大きいほうと小さいほうがあるということですね。ある2つの数 A と B を比較するときには、次のように表すことができます。
(ⅰ) A > B (ⅱ) A < B
それぞれ(i)「 A 大なり B 」、(ii)「 A 小なり B 」と読みます。どちらが大きいかを判断するには、不等号の口が開いているのがどちらであるかに注目しましょう。不等号の口が開いているほうが大きな数を表します。ですから、(ⅰ)は「 A は B より大きい」、(ⅱ)は「 A は B より小さい」ということを表しています。不等号の形からイメージするといいですね。また、(ⅱ)は「 A は B 未満」とも読まれますので、こちらも確実に覚えておきましょう。
「 > 」「 < 」と「 ≧ 」「 ≦ 」の違いは?
「 > 」「 < 」と「 ≧ 」「 ≦ 」はどう違うのでしょうか? 記号を見てみると、「 ≧ 」「 ≦ 」は「 > 」「 < 」の下に「 = 」がついていますね。そのままの意味で、『「 ≧ 」は「 > 」と「 = 」を合わせたもの』『「 ≦ 」は「 < 」と「 = 」を合わせたもの』なのです。つまり、等しい関係も含むということです。
(ⅲ) A ≧ B (ⅳ) A ≦ B
(ⅲ)は「 A は B より大きい または A は B と等しい」という意味で、読み方は「 A 大なりイコール B ( A は B 以上)」であり、(ⅳ)は「 A は B より小さい または A は B と等しい」という意味で、読み方は「 A 小なりイコール B ( A は B 以下)」です。「以上」「以下」は等しい関係も含むということがポイントです。「以上、以下のイは、イコールのイ」と覚えると、忘れないですね。
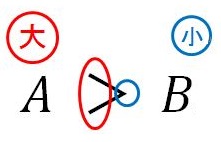
不等号を使って数量の関係を表してみよう!
不等号を使って2つの数量の大小関係を表した式を「不等式」といいます。不等式をたてることで、不等号の使い方を覚えていきましょう。
●例題
次の数量の関係を、不等式で表しなさい。
(1) x は8より小さい。
(2) a は-3以上である。
(3) b の3倍は15以下である。
(4) y から6を引いた数は-5より大きい。
文字と数字が入っていますが、これまでの説明の「 A 」と「 B 」をそのまま置き換えて考えればよいですね。
(1)、(2)はそのまま素直に置き換えればよいですから、答えは以下の通りです。
(1) x < 8 (2) a ≧ − 3
(3)、(4)も同じように考えます。ただし、「 b の3倍」「 y から6を引いた数」を文字式に直して不等式の中に入れなければなりません。
(3) b の3倍は、 3 × b より 3 b なので、答えは 3 b ≦ 15
(4) y から6を引いた数は、 y − 6 なので、答えは y − 6 > − 5
先の単元に進むにつれて、様々な等式や不等式をたてることになります。これが最も基本となる部分です。難しく考えず、素直に式をたてることが大切です。
個別指導塾の基本問題に挑戦!
■問題■
次の数量の関係を、不等式で表しなさい。
(1) x は-12より大きい。
(2) a の4倍は16未満である。
(3) c に6を加えた数は-5以下である。
(4) y を8倍してから3を引いた数は9以上である。
■答え■
(1) x > − 12
(2)「16未満」は「16より小さい」と同じなので、答えは 4 a < 16
(3) c + 6 ≦ − 5
(4)yの8倍は 8 b 、そこから3を引くと 8 b − 3 なので、
答えは 8 b − 3 ≧ 9
様々な数量の関係を表してみよう!
1つ1つ順番に考えて不等式をたてよう!
次は、日常的な題材を使った問題で不等式をたててみましょう。
●例題
次の数量の関係を、不等式で表しなさい。
(1)1本150円のペン x 本と、1個80円の消しゴムを2個買ったところ、代金の合計は800円以下だった。
(2)底辺が 8 c m 、高さが a c m の三角形の面積が 20 c m 2 よりも大きい。
先ほどの問題に比べると少し難しそうに感じますね。基本的な考え方は同じです。1つ1つ順番に考えていきましょう。
(1)は、「代金の合計は800円以下」とありますね。ですから、「(代金の合計) ≦ 800 」とすればいいですね。では「代金の合計」を式で表して不等式をたてましょう。
(1本150円のペン x 本)+(1個80円の消しゴムを2個)なので、 150 × x + 80 × 2 ≦ 800
このまま答えにしてはいけませんね。文字式のルールに従えば、答えは 150 x + 160 ≦ 800 となります。
(2)は、「面積が 20 c m 2 よりも大きい」とありますね。ですから、「(面積) > 20 」とすればいいですね。
「面積」を式で表して不等式をたてると、(三角形の面積) = (底辺) × (高さ) ÷ 2 なので、
8 × a ÷ 2 > 20
したがって、答えは 4 a > 20 となります。
まず「▲▲が●●よりも~」などの大小の関係に注目して、それから式で表す部分について考えています。このように、1つ1つ順番に考えることが大切です。
個別指導塾の基本問題に挑戦!
■問題
次の数量の関係を、不等式で表しなさい。
(1)1枚30円のせんべい x 枚と1本40円のジュース y 本の代金の合計は、400円よりも高かった。
(2) 800 m の道のりを分速 x m で歩くと、10分かからなかった。
□答え
(1)(代金の合計) > 400 であり、(代金の合計) = (せんべいの代金) + (ジュースの代金) なので、 30 × x + 40 × y > 400
答えは 30 x + 40 y > 400
(2)「~~で歩くと10分かからなかった」すなわち「歩いた時間は10分より短い」ということなので、(歩いた時間) < 10
(時間) = (距離) ÷ (速さ) なので、 800 ÷ x < 10
答えは800/x<10
個別指導塾の応用問題に挑戦!
それでは最後に、実力をつけていくための問題に挑戦しましょう。
■応用問題
次の数量の関係を、不等式で表しなさい。
(1) m に3を加えて2でわった数は4より大きい。
(2) 3 k m の道のりを分速 a m で10分歩いたので、残りの道のりは 800 m 以下になった。
(3)十の位が x 、一の位が y の2桁の整数があり、この整数は y の6倍未満である。
□答え
(1) ![]()
(2) 3000 − 10 a ≦ 800
(3) 10 x + y < 6 y
応用問題が解けなかったお子さんは、「どこがわからないのか」を特定し、基礎からステップを追って確実に復習することが大切です。今回は不等号の意味と、不等式のたて方について解説しました。
この内容では、
・不等号の左側と右側のどちらが大きいかがわからない
・「以上」「以下」と「より大きい」「より小さい」の区別がつかない
・文字式の表し方がわからない
など、つまずくポイントはお子さんによってさまざまです。
場合によっては算数の内容にさかのぼって復習をする必要があるかもしれません。
数学は「積み上げ学習」と言われており、以前の学年で習った内容をもとに、発展した学習を積み上げていきます。特に、今回学んだ、不等号や不等式のたて方は、今後の学習内容にも関わります。できるだけ「わからない」を残さないように、きちんと身につけておきましょう。
中学生の個別指導
目標達成を自分のペースで。1人ひとりに最適な学習プランを組み立て、着実なステップアップを応援します。高校受験、私立補習・内部進学、定期テスト、英検対策までお任せください。
















