数学では2つの数量の関係について多く学びます。中学1年では、「比例」と「反比例」について学びます。「比例」は比較的すんなりと理解できるものの、「反比例」には苦手意識を持つお子さんは多くいます。ここで反比例の意味・式・グラフについて、特徴をしっかりとおさえておきましょう。
反比例の式・グラフをしっかりマスター!中学生の個別指導はこちら⇒

LINE友だち追加で、受験&勉強の最新情報をGET!!
受験や勉強の最新情報をギュっと凝縮した記事を配信中♪学習のお悩みを解決するヒントとなる記事や、東京個別・関西個別からのお知らせもお届け。ぜひご登録ください。
目次
反比例ってどんな関係のこと?
まずは比例について確認!
2つの数量の関係を表すとき、多くの場合はxやyの文字を使って表します。まずは比例についてxやyの関係を見てみましょう。
|
xの値が2倍、3倍・・・になると、yの値が2倍、3倍・・・になる。 このとき、yはxに比例するという。 |
例えば、「1個20円のアメをx個買ったときの代金をy円」とすると、アメの個数が2倍、3倍・・・になると、代金が2倍、3倍・・・になるので、yはxに比例しています。
この関係を式にしてみると、(代金)=(アメ1個の値段)×(アメの個数)より、y=20xとなります。
2つの数量が比例の関係であるときは、このような形の式で表されます。この式の20のことを比例定数と言い、条件によってこの比例定数は変わります。この比例定数は、文字aで表すことが多く、比例の式は、次のように書き表されます。
| 比例の式 y=αx |
αには正の数だけでなく、負の数も入ることに注意しましょう。
それでは、反比例についてみていきましょう。
反比例の意味と式は?
反比例は、次のように表現されます。
|
xの値が2倍、3倍・・・になると、yの値が このとき、yはxに反比例するという。 |
たとえば、「面積が24cm2である長方形のたての長さをxcm、横の長さをycm」としましょう。比例のときと違い、少々イメージがしにくいかと思います。 そこで、たての長さと横の長さの関係を表にまとめてみましょう。
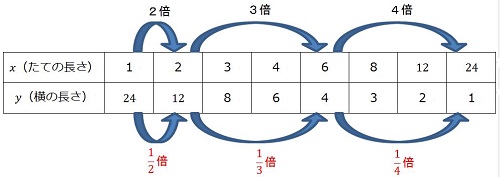
いかがでしょうか?
xの値が2倍のときyの値は![]() 倍、xの値が3倍のときyの値は
倍、xの値が3倍のときyの値は ![]() 倍、xの値が4倍のときyの値は
倍、xの値が4倍のときyの値は ![]() 倍、となっていることが分かりますね。このような関係のとき、yはxに反比例するといいます。
倍、となっていることが分かりますね。このような関係のとき、yはxに反比例するといいます。
では、これを式に表してみましょう。
(たての長さ)×(横の長さ)=(長方形の面積)より、xy=24
ここで、xは0ではないので、両辺をxで割ってみると、 y= ![]() となります。
となります。
2つの数量が反比例の関係であるときは、このような形の式で表されます。
この式の24のことも比例定数と言います。これも、条件によってこの比例定数は変わります。
この比例定数も、文字αで表すことが多く、比例の式は、次のように書き表されます。
| 反比例の式 y= |
こちらも、αには正の数だけでなく,負の数も入ります。この関係式が非常に重要なのです。今後もいろいろな関係式が出てきます。「反比例」と言われたら、すぐに「 y= ![]() 」と答えられるようにしておきましょう。
」と答えられるようにしておきましょう。
反比例の式や値はどうやって求めるの?
では、反比例の式や値の求め方を見ていきましょう。
■例題
yはxに反比例し、x=2のときy=6である。
(1) yをxの式で表しなさい。
(2) x=-4のときのyの値を求めなさい。
「yはxに反比例し」ですから、「 y= ![]() 」の式を使います。解き方は以下の通りです。
」の式を使います。解き方は以下の通りです。
(1):x=2,y=6を y= ![]() に代入しaの値を求め、その値を y=
に代入しaの値を求め、その値を y= ![]() に代入する。
に代入する。
(2):(1)で求めた式に、x=-4を代入する。
「代入する」というのが何回か出てきていますね。そう、この「代入する」というのが基本なのです。
□答え
(1)
x=2,y=6を代入すると、 6= ![]()
両辺を2倍して、a=6 × 2=12
したがって、求める式は y= ![]()
(2)
y= ![]() に、x=-4を代入すると、 y=
に、x=-4を代入すると、 y= ![]() =-3
=-3
個別指導塾の基本問題に挑戦!
■問題
yはxに反比例し、x=-8のときy=2である。
(1) yをxの式で表しなさい。
(2) x=4のときのyの値を求めなさい。
□答え
(1) x=-8、y=2を代入すると、 2= ![]()
両辺を-8倍して、α=2 × (-8)=-16
したがって、求める式は y= –![]()
(2) y= –![]() に、x=4を代入すると、 y=
に、x=4を代入すると、 y= ![]() =-4
=-4
反比例のグラフ
反比例のグラフってどんな形?
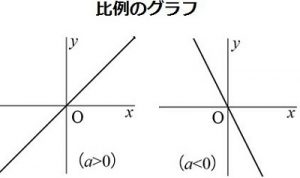
比例のグラフは、原点を通る直線です。比例定数aの値が正のときは右上がり、負のときは右下がりになります。
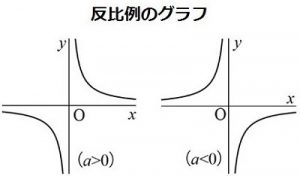
一方、反比例のグラフは直線ではなく、曲線です。反比例のグラフは1つの式につき、2つの曲線からなるので、「双曲線」と呼ばれます。比例定数αの値が正のときはx軸とy軸で区切られた部分の右上と左下、負のときは左上と右下にそれぞれ曲線があります。
また、反比例はどんなにグラフをのばしても、x軸にもy軸にもつきません。これも反比例のグラフの大きな特徴です。
反比例のグラフの書き方は?
グラフの書き方の基本は、「点を打ってそれを結ぶこと」です。比例の場合は直線ですので、点を打ったあと定規でまっすぐ線を引けばよいのですが、反比例は曲線ですから難しいですね。よって、反比例のグラフの場合は、「できるだけ点を打って、双曲線の形になるように、滑らかに線を結ぶ」ようにします。
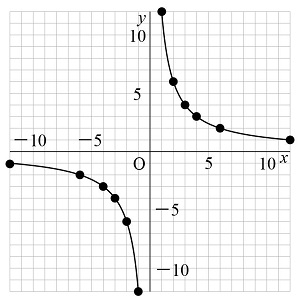
では、具体的に、 y= ![]() のグラフを書いてみましょう。グラフ用紙に書かれている線は一般的に、xの値とyの値が整数になるところですから、 y=
のグラフを書いてみましょう。グラフ用紙に書かれている線は一般的に、xの値とyの値が整数になるところですから、 y= ![]() を成り立たせるxの値とyの値が共に整数である組合せを考えます。
を成り立たせるxの値とyの値が共に整数である組合せを考えます。
表にしてみると、以下の組み合わせがあります。負の値も含むこと、分母に0を入れることはできないことにも注意しましょう。

まずは点を打っていくと、次の左側の図のようになりますね。そして、滑らかに線を結んでいくと右側の図のようになります。このときに気をつけなくてはいけないポイントは2つです。
|
ポイント
|
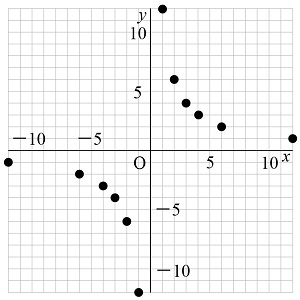
「滑らかに書く」というのは難しいかもしれませんが、繰り返し練習することが大事です。
個別指導塾の基本問題に挑戦!
■問題
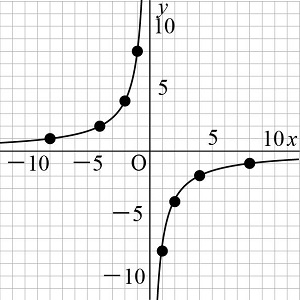
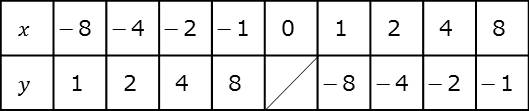
y= –![]() のグラフを書きなさい。(方眼紙など目盛りのある用紙に書いてみましょう。)
のグラフを書きなさい。(方眼紙など目盛りのある用紙に書いてみましょう。)
□答え
個別指導塾の応用問題に挑戦!
それでは最後に、実力をつけていくための問題に挑戦しましょう。
■応用問題
下の図は反比例 y= ![]() のグラフを表している。点A、B、Cはいずれも y=
のグラフを表している。点A、B、Cはいずれも y= ![]() のグラフ上の点である。以下の問いに答えなさい。
のグラフ上の点である。以下の問いに答えなさい。
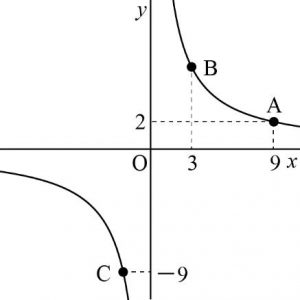
(1) 式のαの値を求めなさい。
(2) 点Bの座標を求めなさい。
(3) 点Cの座標を求めなさい。
□答え
(1) a=18 (2) B (3,6) (3) C (-2,-9)
応用問題が解けなかったお子さんは、「どこがわからないのか」を特定し、基礎からステップを追って確実に復習することが大切です。
今回は反比例の式とグラフについて解説をしました。この内容については、
・反比例の式に代入をして計算することができない
・グラフを書いたり、グラフから式を求めたりすることができない
など、つまずくポイントはお子さんによってさまざまです。場合によっては算数の内容にさかのぼって復習をする必要があるかもしれません。
数学は「積み上げ学習」と言われており、以前の学年で習った内容をもとに、発展した学習を積み上げていきます。特に、今回学んだ、反比例の式の求め方やグラフの書き方は、今後の学習内容にも関わります。できるだけ「わからない」を残さないように、きちんと身に付けておきましょう。
中学生の個別指導
目標達成を自分のペースで。1人ひとりに最適な学習プランを組み立て、着実なステップアップを応援します。高校受験、私立補習・内部進学、定期テスト、英検対策までお任せください。
















