日常生活の中でいろいろな形の図形を見かけます。正三角形や正方形などの正多角形や長方形のように、並べたときに美しく見える形の図形は模様やデザインによく使われます。今回のテーマである「点対称な図形」もその1つです。ただ、「線対称な図形」と「点対称な図形」を区別できていない子がよく見受けられます。ここで、「点対称な図形」について確認をしておきましょう。

LINE友だち追加で、受験&勉強の最新情報をGET!!
受験や勉強の最新情報をギュっと凝縮した記事を配信中♪学習のお悩みを解決するヒントとなる記事や、東京個別・関西個別からのお知らせもお届け。ぜひご登録ください。
目次
「点対称な図形」とは何? どんな性質があるの?
線対称・点対称とは?
今回のテーマは「点対称」ですが、よく「線対称」と混乱してしまう人がいます。まずは、線対称と点対称の区別ができるようにしましょう。線対称は次のように表現されます。
| 1つの直線を折り目にして二つ折りにしたとき、両側の部分がピッタリ重なる図形を線対称な図形という。また、その折り目にした直線を対称の軸という。 |
たとえば、二等辺三角形は次の図のように折ると、ピッタリ重なります。ですから、二等辺三角形は線対称な図形です。この折り目とした線が対称の軸です。一方、平行四辺形を下の図のように折るとピッタリ重なりません。折り目を変えたとしても、ピッタリ重なることはありません。したがって、平行四辺形は線対称な図形ではありません。
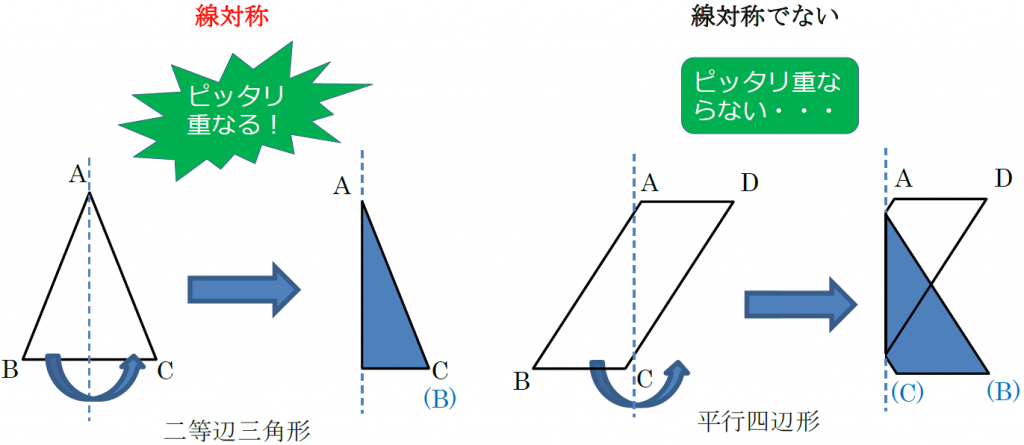
線対称な図形では、対称軸を折り目として二つ折りしたときに重なり合う点、辺、角のことをそれぞれ、「対応する点」「対応する辺」「対応する角」といいます。上の二等辺三角形でいうと、点Bと点Cが重なり合うので、点Bと点Cは対応する点です。
では、点対称について見ていきましょう。次のように表現されます。
| 1つの点のまわりに180°回転させたとき、もとの図形にピッタリ重なる図形を点対称な図形という。また、その点を対称の中心という。 |
たとえば、二等辺三角形を下のように180°回転させると、もとの図形にピッタリ重なりません。どこの点を中心に回転させたとしても、ピッタリ重なることはありません。一方、平行四辺形は、2つの対角線を結んで交わった点を中心に180°回転させるとピッタリ重なります。したがって、平行四辺形は点対称な図形です。このとき、2つの対角線を結んで交わった点が対称の中心です。
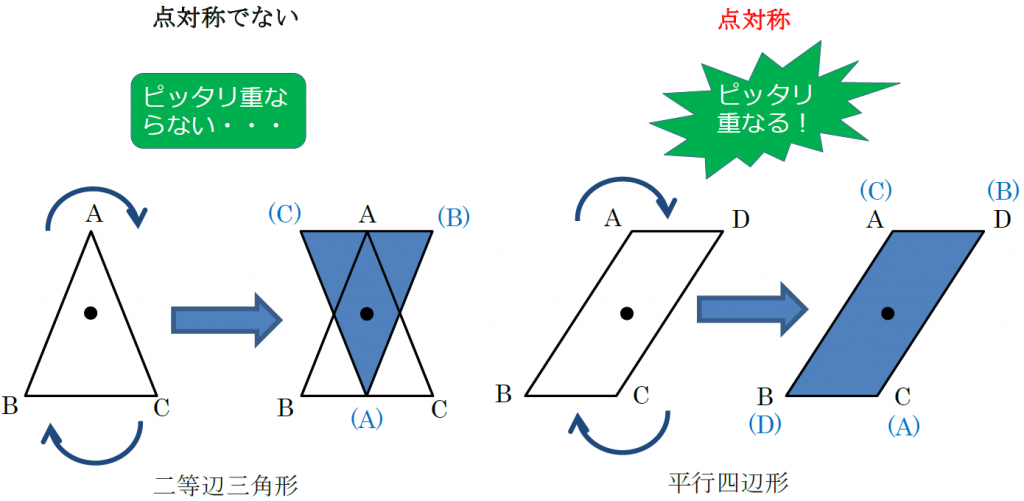
点対称な図形では、対称の中心のまわりに180°回転させたときに重なり合う点、辺、角のことをそれぞれ、「対応する点」「対応する辺」「対応する角」といいます。線対称のときと同じで重なり合う部分のことを「対応する~~」といいます。上の平行四辺形では、点Aと点Cが、点Bと点Dがそれぞれ対応する点といえます。
ここで1つ注意です。点対称な図形は、あくまでも「180°回転させたとき」にピッタリ重なる図形です。正三角形は120°まわすとピッタリ重なりますが、180°まわすとピッタリ重なりません。ですから、正三角形は点対称な図形とはいえません。よく間違えるところですから、お子さんが正しく理解できているか注意して見てあげてください。
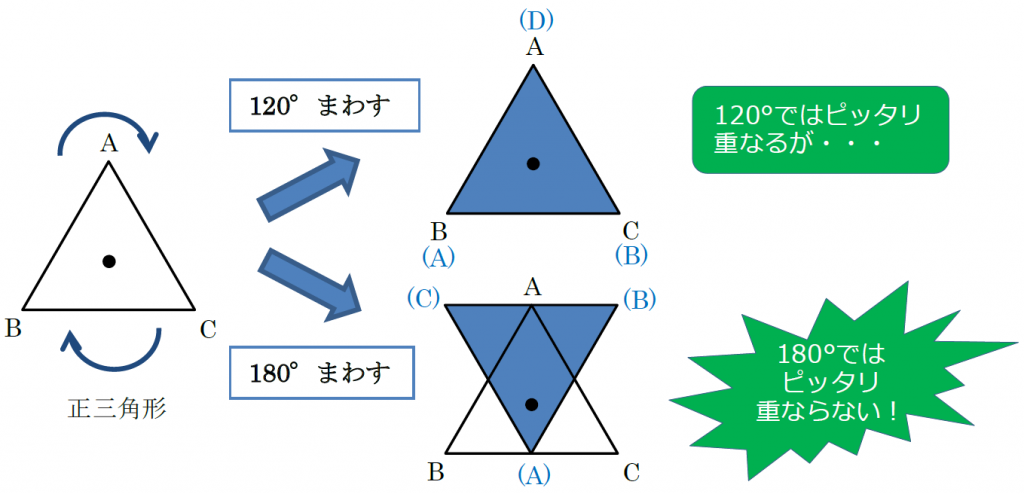
「線対称」のときは折ってピッタリ重なる図形、「点対称」のときは180°回転してピッタリ重なる図形と覚えればよいですね。「線」「点」というキーワードを大事にしましょう。
点対称な図形にはどんな性質があるの?
点対称な図形について詳しく見ていきましょう。次のような性質があります。
| (ⅰ)点対称な図形では、対応する2つの点を結ぶ直線は、対称の中心を通る。 (ⅱ)対称の中心から対応する2つの点までの長さは等しい。 |
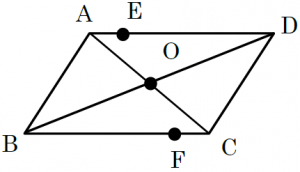
下の平行四辺形ABCDを例に見てみましょう。対称の中心をOとします。
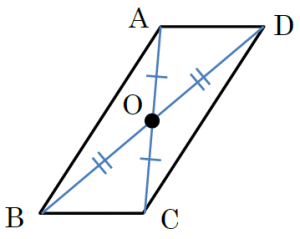
(ⅰ)は、点Aと点C、点Bと点Dをそれぞれ結ぶと、その直線はともに対称の中心Oを通るということです。(ⅱ)は、AOとCO、BOとDOがそれぞれ等しいということです。
この2つの性質はとても大切です。お子さんが正しく理解して覚えているか、確認するとよいでしょう。
点対称な図形かどうかを見分けるには?
180°まわしてピッタリ重なるかを見よう!
点対称な図形であるかどうかを見分ける問題はよく出てきます。例題を通して、どうやって見分けるか見ていきましょう。
|
《例題》
|
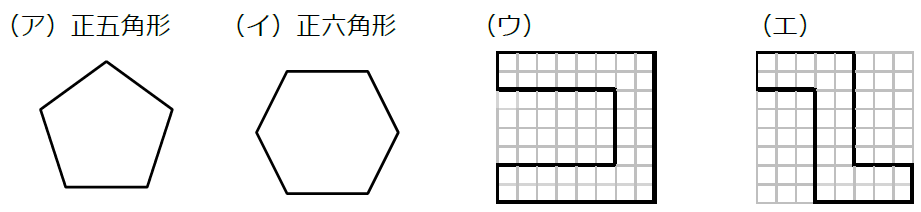
点対称な図形であるかどうかを見分けるには、180°まわして考えます。もとの図形と、それぞれの図形を180°まわしたものを重ね合わせると下の図のようになります。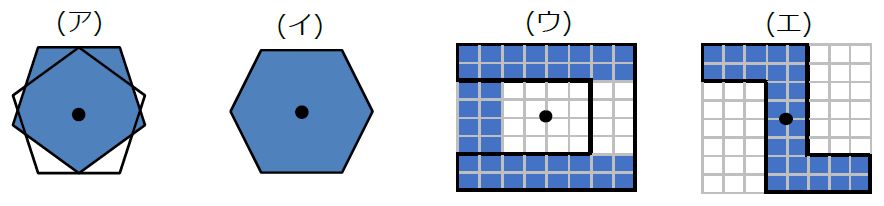
(イ)と(エ)がピッタリ重なっていますね。よって、
(ア)×(イ)○(ウ)×(エ)○
となります。
個別指導塾の基本問題に挑戦!
|
《問題》
|
《答え》
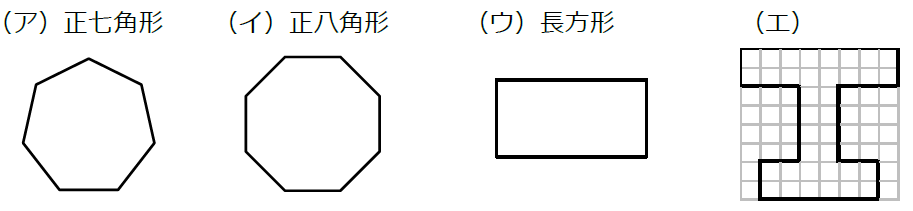
もとの図形と、それぞれの図形を180°まわしたものを重ね合わせると下の図のようになる。
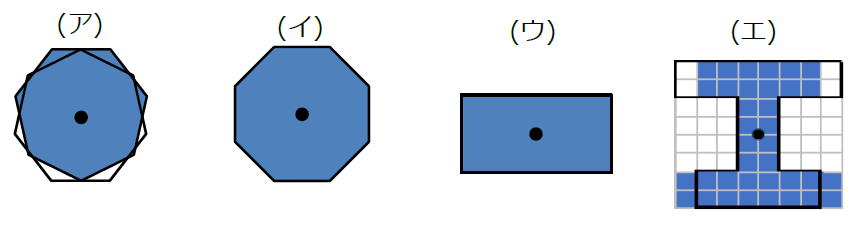
よって、(ア)×(イ)○(ウ)○(エ)×
さて、実際に紙に作図してまわしてみればわかりますが、それができない場合、本当にピッタリ重なるかどうか迷うときもあるかと思います。そのときは、図形の性質の(ⅰ)を利用します。
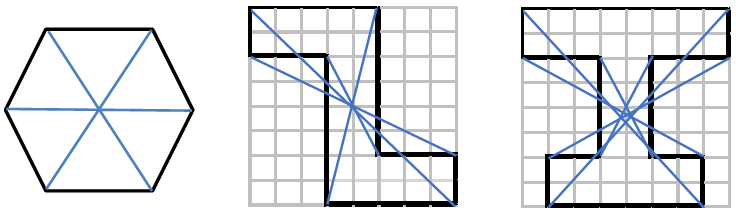
180°まわしたときに重なりそうな(対応する点になりそうな)2点を結んでみます。そのとき、結んだ線が全て1点で交われば、点対称な図形と言えます。1点で交わらなければ、点対称な図形でないと言えます。
ただし、結んだ線が2つだけのときはこれだけでは判断できません。対称の中心からの距離が等しくなっているかも調べる必要があるので注意してください。
数学の「わからない」ところを把握した
効率的・効果的な学習法なら個別指導塾へお任せ
点対称な図形を作図してみよう!
点対称な図形の性質を利用して作図!
点対称な図形を作図する問題に取り組んでみましょう。
|
《例題》
|
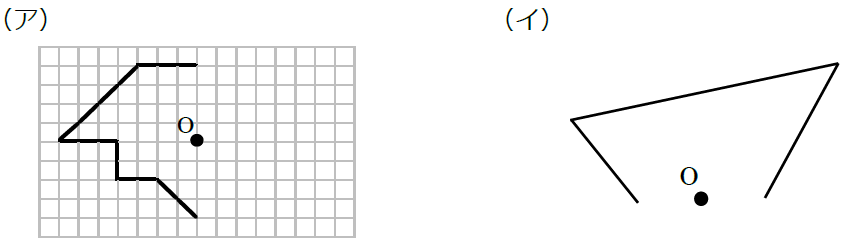
点対称な図形を作図するには、点対称な図形の性質の(ⅱ)対称の中心から対応する2つの点までの長さは等しい を使います。
(ア)は目もりがありますので、それを利用しましょう。図のように1つの頂点をAとします。点Aから点Oへは右へ3つ、下へ4つ進みます。そこから同じ分だけ進んだところが、点Aと対応する点になります。それを他の頂点についても行い、対応する点を見つけます。その点を結んだ図形が答えとなります。
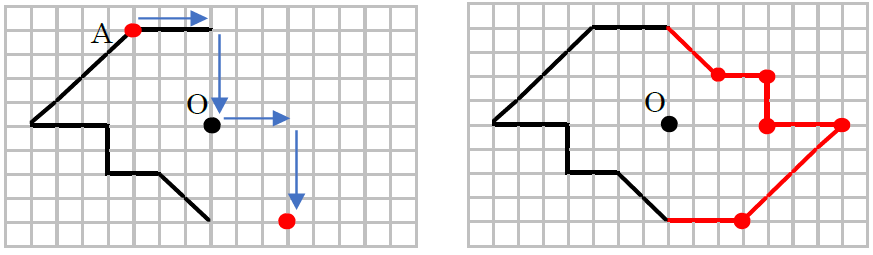
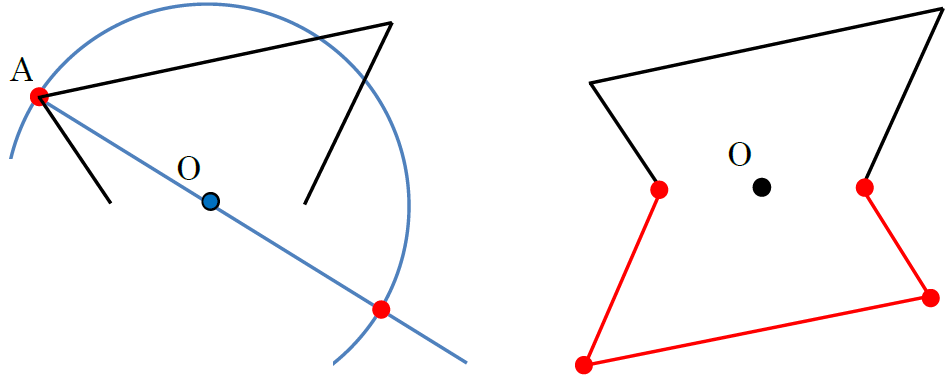
(イ)のように目もりがない場合は、コンパスを使いましょう。まず、点Aから点Oを通る直線をひきます。次にコンパスの針を点Oにおき、点Aを通る円の一部をかき、ひいた直線と交わったところが、点Aと対応する点になります。他の頂点についても同じようにして、対応する点を見つけます。その点を結んだ図形が答えとなります。
個別指導塾の基本問題に挑戦!
|
《問題》
|
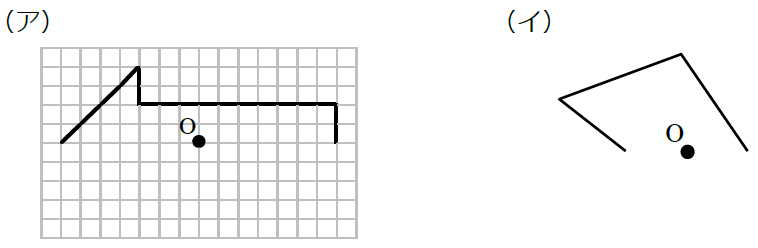
《答え》
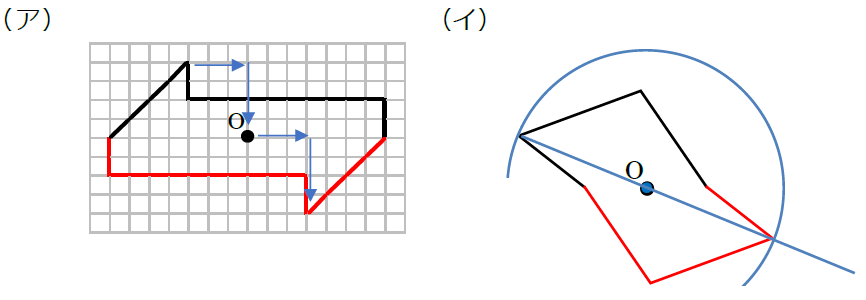
上と同じように各点の対応する点を1つずつ見つけて、その点を結びましょう。答えは下の図の通りです。(点を見つけるための矢印や作図の線を一部入れています。)
個別指導塾の応用問題に挑戦!
|
《問題》
(1)辺ABに対応する辺を答えなさい。 |
《答え》
(1)辺CD (2)5cm (3)10cm
《解説》
(1)対応する順番に注意。点Aと対応する点はC、点Bと対応する点はDだから、辺CDとなる。
(2)点Aと点Cは対応しており、対称の中心から対応する2つの点までの長さは等しいので、点OはACの中点なので、AO=10÷2=5(cm)
(3)線分CFは線分AEと対応しているから、CF=2cm。よって、
BF=BC-CF=12-2=10 (cm)
応用問題が解けなかったお子さんは、「どこがわからないのか」を特定し、基礎からステップを追って確実に復習することが大切です。今回は点対称な図形について解説しました。この内容では、
・点対称な図形であるかどうかが判断できない。
・対応する点を見つけることができない。
・点対称な図形の性質を利用した問題が解けない。
など、つまずくポイントはお子さんによってさまざまです。
数学は「積み上げ学習」と言われており、以前の学年で習った内容や算数の内容をもとに、発展した学習を積み上げていきます。特に、今回学んだ、点対称な図形の性質は身についている知識として、当然のように問題に出てくることがあります。できるだけ「わからない」を残さないように、きちんと身につけておくようにしましょう。