数学の図形分野では、形、長さ、面積、体積など、さまざま様々な図形の特徴や性質について扱います。これらは、長さを推測するときや、図形の面積や体積を知るときに大いに役立っています。
中学3年生で扱う「中点連結定理」は、ある条件を満たす場合の線分の長さなどを求めるときに、強力な武器になります。名前だけを見ると難しそうに感じられますが、実はとても簡単な定理です。中点連結定理とその使い方について確認しましょう。

LINE友だち追加で、受験&勉強の最新情報をGET!!
受験や勉強の最新情報をギュっと凝縮した記事を配信中♪学習のお悩みを解決するヒントとなる記事や、東京個別・関西個別からのお知らせもお届け。ぜひご登録ください。
目次
中点連結定理を使って長さを求めよう!
中点連結定理とは?
「中点連結定理」とは以下のように表現されます。
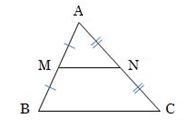
△ABCの2辺AB、ACの中点をそれぞれM、Nとすると、次の関係が成り立つ。
MN//BC ![]()
式で表されるとちょっとわかりにくいですね。
「三角形の底辺でない2つの辺の中点を結んでできた線分は、底辺と平行で、その長さは底辺の半分である。」
ということです。

もっと簡単に、「中点同士を結んだら、底辺と平行で長さは半分」と覚えればよいです。例えば、
・底辺BCの長さが16cmのとき、MNの長さは16cmの半分の8cm
・MNの長さが5cmのとき、底辺BCの長さは5cmの2倍の10cm
となります。
三角形で中点連結定理を使って長さを求めるのは、比較的やさしいですね。では、よくある問題として、台形での中点連結定理の利用についてみていきましょう。
台形で中点連結定理を利用する!
●例題
下の図のように、ADの長さが6cm、BCの長さが12cm、AD// BCである台形ABCDがある。辺AB、DCの中点をそれぞれE、Fとする。このとき、EFの長さを求めなさい。
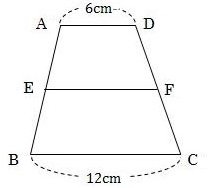
この問題は、中点連結定理を利用して導かれるある性質によって、簡単に解くことができます。
下の図のように、BCを延長した直線と直線AFの交点をGとします。
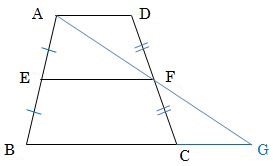
このとき、△ADFと△GCFは合同ですから、AF=GF、AD=GCがいえます。
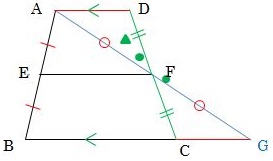
次に△ABGに注目します。AF=GFよりFはAGの中点、AD=CGとBG=CG+BCより、BG=AD+BCといえます。
すると、点EとFはそれぞれの辺の中点ですから、中点連結定理より、![]() 、すなわち、
、すなわち、![]() となります。
となります。
これは、「台形の平行でない対辺の2つの辺の中点を結んだ線分は、上底と下底を合わせた長さの半分である。」ということを表しています。
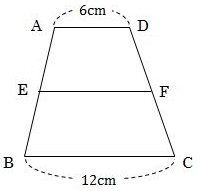
問題に戻ると、上底のADの長さは6cm、下底のBCの長さは12cm、したがって、
![]() となります。
となります。
個別指導塾の基本問題に挑戦!
■問題
(1)下の図のように、△ABCにおいて、辺BC、CA、ABの中点をそれぞれD、E、Fとする。BC=9cm、CA=7cm、DE=3cmであるとき、AB、DFの長さをそれぞれ答えなさい。
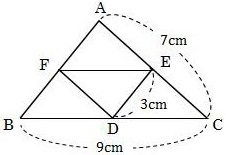
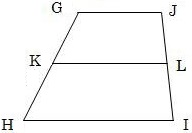
(2)GJの長さが5cm、HIの長さが9cm、GJ//HIの台形GHIJがある。辺GH、JIの中点をそれぞれK、Lとする。このとき、KLの長さを求めなさい。
□答え
(1)頂点をCとして考えると底辺はAB。
中点連結定理より、ABはDEの2倍なので、
AB=6cm。
Bを頂点として考えると底辺はCA。
中点連結定理より、DFはCAの半分なので、
![]()
(2)台形の上底と下底をそれぞれGJ、HIとする。K、LはそれぞれGH、JIの中点だから、
![]()
中点連結定理を利用した証明をしてみよう!
中点連結定理を利用して平行四辺形であることを証明しよう!
中点連結定理を利用して、平行四辺形やひし形のような特別な四角形であることを証明することができます。証明問題は苦手な人が多いと思いますが、ここでの証明はパターンがある程度決まっていますから、その流れをつかんでしまいしょう。
●例題
右の図のような四角形ABCDがあり、点E、F、G、Hはそれぞれ各辺の中点であるとする。このとき、四角形EFGHが平行四辺形であることを証明しなさい。
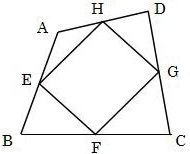
各辺の中点を結んだ線分でできた四角形が平行四辺形であることを証明します。ここでのポイントは2つです。
(ⅰ)対角線を1本引いて、2つの三角形について中点連結定理を使う。
(ⅱ)平行四辺形になるための条件のうち「1組の対辺が平行で長さが等しい」を使う。
このことをまず頭に入れておきましょう。
ACとBDのどちらでもよいのですが、ここでは対角線ACで考えます。△ABCと△ADCのそれぞれに着目すると、ACが共通しているので、ACを底辺と考えましょう。
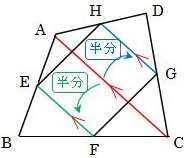
・△ABCにおいて、EFはACと平行で長さはACの半分。
・△ADCにおいて、HGはACと平行で長さはACの半分。
この2つをみて何か気づきませんか? 次のことが言えますね。
・EFとHGはともにACと平行 ⇒ EFとHGは平行
・EFとHGの長さはともにACの半分 ⇒ EFとHGは等しい
ここで、EFとHGは四角形EFGHの対辺ですから、「1組の対辺が平行で長さが等しい」ということが言えますね。では、きちんとした証明の書き方をみていきましょう。
□答え
証明
対角線ACを引く。
△ABCにおいて、E、FはそれぞれBA、BCの中点だから、
中点連結定理より、EF//AC……① ![]() ……②
……②
△ADCにおいて、G、HはそれぞれDC、DAの中点だから、
中点連結定理より、HG//AC……③ ![]() ……④
……④
①、③より、EF//HG……⑤
②、④より、EF=HG……⑥
⑤、⑥より、1組の対辺が平行で長さが等しいので、四角形EFGHは平行四辺形である。
(証明終わり)
最初から自分で証明できるようになるというのは難しいかと思いますが、大事なのは、書き方のパターンを身につけることと、解く方針をたてることです。今回の問題のように補助線が必要となることもありますが、まず、知っていることが使えないかを考えることが大切です。
続いては先ほどの問題の類題です。対角線BDをひくところから証明していきましょう。
個別指導塾の基本問題に挑戦!
■問題
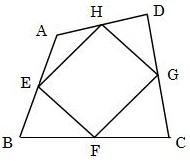
下の図のような四角形ABCDがあり、点E、F、G、Hはそれぞれ各辺の中点であるとする。このとき、四角形EFGHが平行四辺形であることを、以下のように証明した。( )内にあてはまる式や言葉を答えなさい。
証明
対角線BDをひく。
△ABDにおいて、E、Hはそれぞれ(ア)、(イ)の中点だから、
中点連結定理より、(ウ)//BD……① (エ)![]() ……②
……②
△CDBにおいて、(オ)、(カ)はそれぞれCF、CGの中点だから、
中点連結定理より、FG//(キ)……③ ![]() ……④
……④
①、③より、(ケ)//FG……⑤
②、④より、EH=(コ)……⑥
⑤、⑥より、(サ)ので、四角形EFGHは平行四辺形である。
(証明終わり)
□答え
ア:AB イ:AD ウ:EH エ:EH オ:F カ:G キ:BD ク:BD ケ:EH コ:FG サ:1組の対辺が平行で長さが等しい
個別指導塾の応用問題に挑戦!
■問題
下の図の△ABCにおいて、点D、Eは辺ABを3等分する点である。また、点Fは辺ACの中点であり、点Gは直線BCと直線DFの交点である。このとき、次の問いに答えなさい。
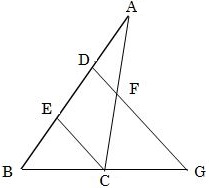
(1)BC=CGであることを証明しなさい。
(2)FGはECの何倍か。
□答え
(1)証明
△AECにおいて、D、FはそれぞれAE、ACの中点なので、
中点連結定理より、DF//EC
△BDGにおいて、EC//DGより、平行線と比の性質から、
BC:CG=BE:ED=1:1
したがって、BC=CG
(証明終わり)
(2)![]()
応用問題が解けなかったお子さんは、「どこがわからないのか」を特定し、基礎からステップを追って確実に復習することが大切です。今回は中点連結定理について解説をしました。
この内容については、
・中点連結定理の意味がわからない
・中点連結定理を使うのに、どの辺を底辺としてみるのかがわからない
・証明の仕方がわからない
など、つまずくポイントはお子さんによってさまざまです。
場合によっては小学校で習う三角形の性格や、中学1・2年生の内容にさかのぼって復習をする必要があるかもしれません。
数学は「積み上げ学習」と言われており、以前の学年で習った内容をもとに、発展した学習を積み上げていきます。特に、今回学んだ中点連結定理は、今後の学習内容や入試にも関わります。できるだけ「わからない」を残さないように、きちんと身につけておきましょう。
中学生の個別指導
目標達成を自分のペースで。1人ひとりに最適な学習プランを組み立て、着実なステップアップを応援します。高校受験、私立補習・内部進学、定期テスト、英検対策までお任せください。
















