2つの図形がぴったりと重なり合うとき、その2つの図形は合同である、といいます。ですから、2つの図形の形や大きさは同じです。位置や向きを変えるだけでぴったり重なる図形を合同といいます。そのため、2つの図形が合同であるかどうかを判断するには、2つの図形を重ねればよいのですが、それができるとは限りません。
合同かどうかの判断方法を学ぶのが「三角形の合同条件」の単元です。しかし、「条件が覚えられない」「どこをみればよいのかがわからない」などでつまずくお子さんがいらっしゃいます。ここでは、三角形が合同になるときの条件、さらには、特別な三角形の1つである直角三角形の合同になるときの条件をみていきます。後の単元では、知っていて当然として出てきますので、ここでしっかりと覚えられるようにしてあげてください。
三角形の合同条件しっかりマスター!中学生の個別指導はこちら⇒

LINE友だち追加で、受験&勉強の最新情報をGET!!
受験や勉強の最新情報をギュっと凝縮した記事を配信中♪学習のお悩みを解決するヒントとなる記事や、東京個別・関西個別からのお知らせもお届け。ぜひご登録ください。
目次
三角形の合同条件を確認しよう!
三角形の合同条件は3つ!
まずは、三角形が合同になるときの条件をみていきます。2つの三角形が合同かどうかを判断するには、すべての辺や角を調べなくても、ある条件を満たせば、合同であることがいえます。この条件のことを、三角形の合同条件といいます。また、2つの図形が合同であることを式で表すときは、合同を表す「≡」の記号を用います。例えば、△ABC≡△DEFといったようにです。合同条件には、以下の3つの条件があります。まずは、この合同条件を確実に覚えてもらいましょう。
(ⅰ) 3組の辺がそれぞれ等しい。
(ⅱ) 2組の辺とその間の角がそれぞれ等しい。
(ⅲ) 1組の辺とその両端の角がそれぞれ等しい。
この合同条件のうち1つを満たせば、2つの三角形は合同であるといえます。位置が関係するものもありますので、言葉だけでなく図と共に覚えることがポイントです。1つ1つみていきましょう。
(ⅰ) 3組の辺がそれぞれ等しい
3つの辺の長さが決まると、三角形は1通りに決まるので、この条件を満たせば、2つの三角形は合同です。
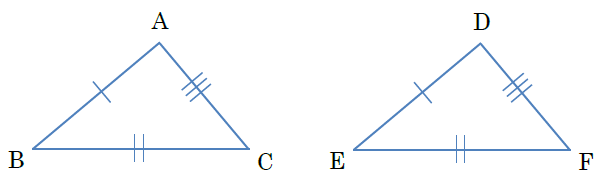
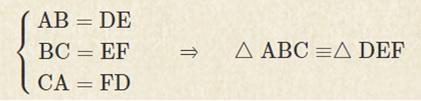
このように、「△○○○」と書く場合は、対応する頂点を同じ順番に書きます。間違いやすいところなので、注意させましょう。
(ⅱ) 2組の辺とその間の角がそれぞれ等しい
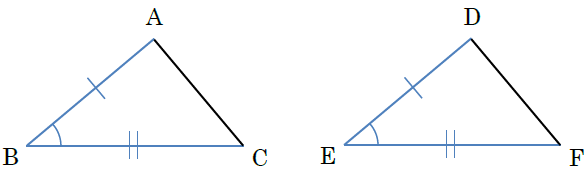
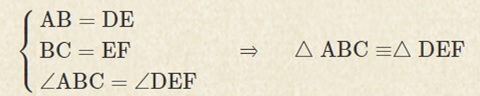
2つの辺の長さと1つの角の大きさが決まれば、三角形は1通りに決まります。よって、この条件を満たせば、2つの三角形は合同です。ただし、2つの辺の間にない角が与えられた場合、三角形が1通りに決まらないことがあるため、合同条件とはなりません。
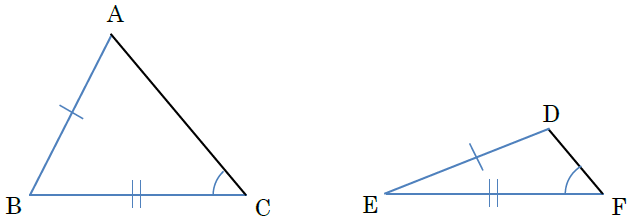
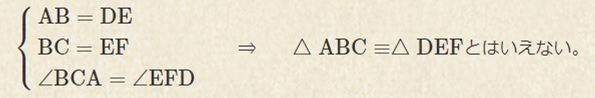
ここが特に間違えやすいところです。よく注意をするようにしてください。合同条件の言葉だけでなく、図と合わせて覚えていくことが大切です。
また、合同条件で「3組の辺がそれぞれ等しい」「2組の辺とその間の角がそれぞれ等しい」「1組の辺とその両端の角がそれぞれ等しい」の「それぞれ」を書き忘れて間違えてしまうお子さんも多くいらっしゃいます。非常にもったいない間違いなので、書き忘れのないよう、十分に気を付けてもらえればと思います。
(ⅲ) 1組の辺とその両端の角がそれぞれ等しい
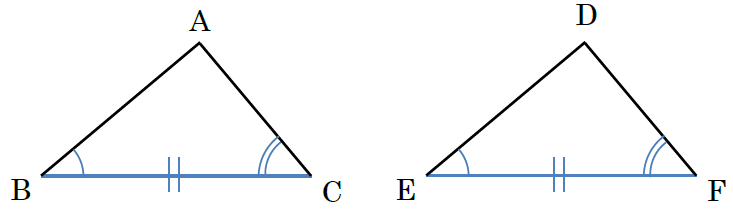
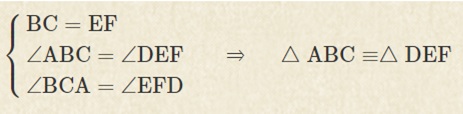
1つの辺の長さとその両端の角の大きさが決まると、三角形は1通りに決まるので、この条件を満たせば、2つの三角形は合同です。
3つの合同条件に共通することは、辺と角を合わせて3か所が等しいということです。これも覚えるときの1つのポイントです。ただし、「3つの角がそれぞれ等しい」という合同条件はありませんので注意がいります。3つの角がそれぞれ等しいだけだと、「相似」とはいえても「合同」とは限りません。たとえば、下の図は3つの角がそれぞれ等しい三角形ですが、ぴったり重ならないので「合同」とはいえませんよね。
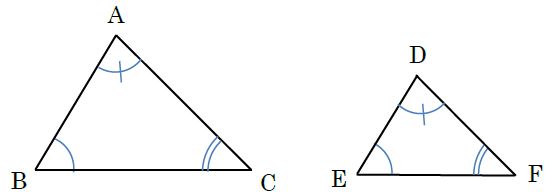
ここも勘違いするお子さんがよくいらっしゃいます。「3つの角がそれぞれ等しい」では合同とはいえない、と注意するよう伝えてあげてください。
東京個別・関西個別(個別指導塾)の基本問題に挑戦!
では、合同条件を確認したところで、合同条件を使って、合同な三角形をみつける問題に取り組み、合同条件の使い方を身につけていきましょう。辺と角の位置をしっかりと確認してもらうことが大切です。
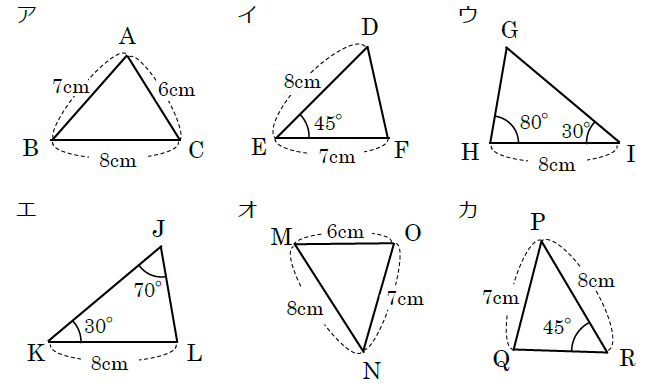
下のア~カにおいて、合同な三角形の組をみつけ、記号≡を使って表しなさい。また、そのときに使った合同条件を書きなさい。
《答え》
・3辺の長さが与えられている三角形アとオに着目します。ともに、6cm、7cm、8cmの長さが与えられていますので、合同条件「3組の辺がそれぞれ等しい」を満たします。ただし、合同の記号を使って表すときには、対応する順に頂点を書く必要があります。
AB=ON=7cm、BC=NM=8cm、CA=MO=6cmなので、
△ABC≡△ONM 合同条件:3組の辺がそれぞれ等しい
・2辺の長さと1つの角の大きさが与えられている三角形イとカに着目すると、ともに、7cm、8cm、45° が与えられています。ただし、イは与えられた2辺の間の角が45°ですが、カは違うところに45°の角があります。よって、合同条件を満たしません。
2つの辺と1つの角の大きさが等しくても、「2組の辺とその間の角」の条件を満たしていませんね。こういった位置関係にも注意するように伝えてあげてください。
・1辺の長さと2つの角の大きさが与えられている三角形ウとエに着目します。ウは、8cmの辺の両端の角が30°と80°です。一方、エは8cmの辺の一方の端に30°があり、離れたところに70°の角があります。三角形の内角の和が180°であることを利用すると、180°-(30°+70°)=80° より、もう一方の端の角が80°であることがわかります。よって、合同条件「1組の辺とその両端の角がそれぞれ等しい」を満たします。
HI=LK=8cm、∠H=∠L=80°、∠I=∠K=30° なので、
△GHI≡△JLK 合同条件:1組の辺とその両端の角がそれぞれ等しい
このように、書かれていない角度や長さを調べることで、正解を導ける場合もあります。
効率的・効果的な学習法なら個別指導塾へお任せ
直角三角形の合同条件とは?
直角三角形の合同条件とは?
次に直角三角形の合同条件についてみていきましょう。三角形の合同条件に加え、新しく覚えなくてはいけないため、なかなか身につかないお子さんがいらっしゃいます。覚えるためのポイントがありますので、それをしっかりと押さえるように伝えてあげてください。
直角三角形とは、1つの角が直角(90°)である三角形のことです。その他の2つの角は90°より小さい鋭角です。また、直角の向かい側の辺(対辺)のことを斜辺といいます。
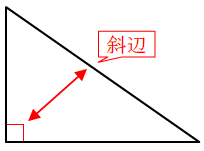
直角三角形にも、三角形の合同条件を使うことができます。ただし、直角を持つという特別な性質から、直角三角形特有の合同条件があるのです。
(ⅰ) 斜辺と1つの鋭角がそれぞれ等しい。
(ⅱ) 斜辺と他の1辺がそれぞれ等しい。
(ⅰ) 斜辺と1つの鋭角がそれぞれ等しい。
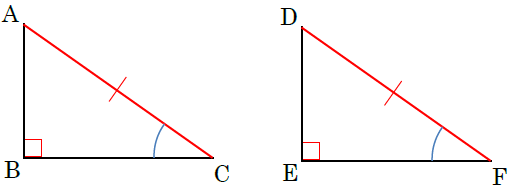

直角三角形で、1つの鋭角が決まれば、もう1つの鋭角の大きさも決まります。すなわち、斜辺とその両端の角が決まるので三角形は1通りに決まります。よって、この条件を満たせば、2つの直角三角形は合同となります。
(ⅱ) 斜辺と他の1辺がそれぞれ等しい。
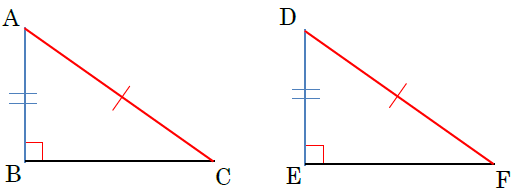

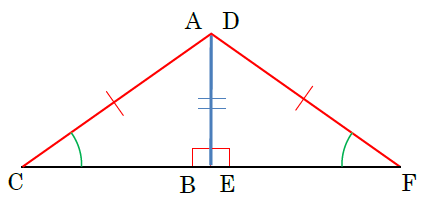
この2つの三角形の一方を裏返してもう一方の三角形と下の図のように重ねます。すると、∠CBA+∠FED=180°になるため、C,B(E),Fは一直線上にあり、二等辺三角形ができます。二等辺三角形の底角は等しいので、∠ACB=∠DFEとなり,三角形の内角の和は180°から∠CAB=∠FDEもいえるので、2辺とその間の角,もしくは1辺とその両端の角がそれぞれ等しいことから、△ABCと△DEFは合同といえます。
このことから、「斜辺と他の1辺がそれぞれ等しい」という条件を満たせば、2つの直角三角形は合同といえます。
さて、この2つの合同条件に共通するのは、「斜辺が等しい」という点です。2つの直角三角形が合同かどうかを判断するには、まず斜辺が等しいかどうかをみて、他に等しい辺や角がないかを確認すればよいのです。斜辺が等しいかどうかがわからなければ直角三角形の合同条件は使えません。「斜辺」+1つの辺 または 1つの角 ということを覚えてもらうのがポイントです。
東京個別・関西個別(個別指導塾)の基本問題に挑戦!
次は合同な直角三角形をみつける問題です。直角三角形の合同条件をよく確認してお子さんと一緒に取り組んでみてください。
下のア~エにおいて、合同な三角形の組をみつけ、記号≡を使って表しなさい。また、そのときに使った合同条件を書きなさい。
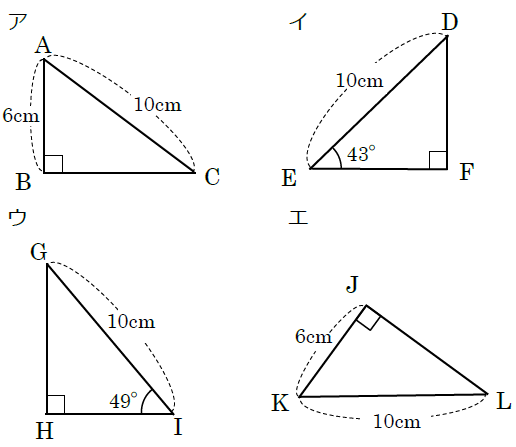
《答え》
いずれも直角三角形で、斜辺の長さはいずれも等しいので、斜辺以外の1辺が与えられているものと、直角以外の1つの鋭角が与えられているもので考えます。
・斜辺以外の1辺が与えられているものはアとエ。その長さはともに6cmなので、直角三角形の合同条件「斜辺と他の1辺がそれぞれ等しい」を満たします。
AB=KJ=6cm、CA=LK=10cmなので、
△ABC≡△KJL 合同条件:斜辺と他の1辺がそれぞれ等しい
・1つの鋭角が与えられているものはイとウ。イに与えられている角は43°。ウに与えられているのは49°で、もう一つの鋭角を求めると、90°ー49°=41° で等しくありません。よって、合同条件は満たしません。
ここまで、三角形の合同条件と直角三角形の合同条件についてみてきました。合同条件を言葉で覚えるのはもちろん、図で位置を確かめることが重要です。また、言葉だけでなく図と一緒のほうが早く覚えられますので、ぜひお試しください。
東京個別・関西個別(個別指導塾)の応用問題に挑戦!
今度は応用問題に取り組んでレベルアップしましょう。図を自分でかいて考えることがポイントです。
次の三角形で、合同な三角形はどれとどれか。記号≡を使って表しなさい。また、そのときに使った合同条件を書きなさい。
・∠B=90°、AB=3cm、CA=5cm の△ABC
・∠E=90°、DE=3cm、EF=5cm の△DEF
・∠I=90°、HI=3cm、GH=4cm の△GHI
・∠K=90°、∠J=40°、LJ=4cm の△JKL
・∠M=90°、∠O=40°、MN=4cm の△MNO
・∠Q=90°、∠R=40°、PR=4cm の△PQR
《答え》
△JKL≡△RQP
合同条件:斜辺と1つの鋭角がそれぞれ等しい
《解説》
頭の中ではなく手を動かして,それぞれを図に表して考えます。三角形の合同条件や、直角三角形の合同条件の「斜辺と他の1辺がそれぞれ等しい」にあてはまるものはなく、「斜辺と1つの鋭角がそれぞれ等しい」にあてはまるものが1組あります。

応用問題が解けなかったお子さんは、「どこがわからないのか」を特定し、基礎からステップを追って確実に復習することが大切です。今回は直角三角形の合同条件について解説しました。
例えば、
・そもそも合同な図形とはなにかがわからない。
・三角形の合同条件を覚えていない。
・直角三角形の斜辺の位置がわからない。
など,知識面のつまずきや、「手を動かして図を書こうとしない」つまずきもあります。つまずくポイントはお子さんによってさまざまです。
数学は「積み上げ学習」と言われており、以前の学年で習った内容や算数の内容をもとに、発展した学習を積み上げていきます。特に、今回学んだ直角三角形の合同条件は身についている知識として、当然のように問題に出てくることもあります。できるだけ「わからない」を残さないように、きちんと身につけておきましょう。

東京個別・関西個別の個別指導
受験合格も、成績アップも。1人ひとりの目標達成をサポート。学習計画から進捗管理まで、お子さまにピッタリの学び方をご提案します。
自由度の高い通塾スタイル&学習環境で、通いやすい、学びやすい個別指導塾です。無料体験・学習相談、受付中!















